5.1 Introduction#
When waves approach the outer slope of a dike they will run up the slope. The highest point that the waves reach is called the run-up level. This point can be considerably above the design water level. If the crest is the dike is below the (theoretical) run-up level, the waves will cause a flow of water over the top of the dike, across the crest and onto the inner slope. This phenomenon is called wave overtopping. Note that this is different from the failure mechanism overflow, which happens when the design water level itself is already higher than the crest level of the dike (also in the absence of waves). While overflow is introduced in these lecture notes, the focus is on run-up and overtopping.
The mean failure mechanism associated with run-up and overtopping is the stability of the inner slope of the levee. Overtopping water can erode the inner slope which can lead to progressive damage and eventually collapse. Typical design options are either to make the inner slope strong enough to cope with the flow of water, or modify the geometry of the dike in such a way that the degree of overtopping is reduced. These options are explored in this chapter.
The central focus of this chapter is the ultimate limit state related to flood safety, i.e. the failure of the levee because of overtopping. There may be reasons other than flood safety to consider. It may for instance be problematic if large volumes of water overtop, even if the dike itself does not fail, or if the crest has to be accessible by emergency vehicles.. The calculation methods described in this chapter can also be used to make assessments in those cases, but the associated criteria may be different (and will have to be developed specifically on a case-by-case basis).
5.1.1 Definitions#
Overtopping is the general term used for the amount of water that passes over the crest of the structure (per linear meter length). It can be expressed as a mean overtopping rate, which is the total volume of water that has passed the crest during a time interval (e.g. an hour), divided by the duration of that interval. Another way to express overtopping is by looking at individual overtopping volume per wave and the resulting flow velocities. This is especially relevant for the assessment of the strength of the inner slope of an overtopped structure.
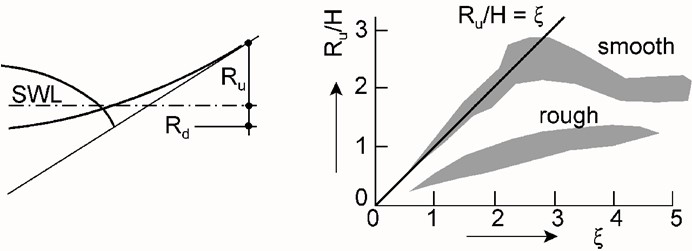
\label{Subsec:iribarren} Both run-up and overtopping depend strongly on whether or not the waves break onto the slope of the structure. This can be described by the Iribarren parameter (also called surf similarity or breaker parameter), \(\xi_{m-1,0}=\tan\alpha/\sqrt{H_{m0}/L_{m-1,0}}\), which relates wave steepness to the slope of a beach (or levee slope). In this case \(H_{m0}\) refers to the (spectral) significant wave height at the location of wave breaking, whereas \(L_{m-1,0}\) is the wave length, \(g T_{m-1,0}^2/(2\pi)\) []. Both the significant wave height \(H_{m0}\) and the (spectral) mean wave period \(T_{m-1,0}\) can be found using computational models like SWAN or 1D approximations like Bretschneider. For small values of this parameter (roughly \(\xi\) < 2) the waves will form spilling or plunging breakers on the slope. For larger values of \(\xi\) the waves will not break, but rather surge onto the slope. The resulting behaviour for both run-up and overtopping is different in these two cases. As a result, the prediction formulas for run-up level and overtopping volumes usually have two different branches to describe these two separate regimes.
Run-up and overtopping are highest on smooth, straight outer slopes. They decrease when the slope is covered with rough elements, or has some permeability. Also berms halfway up the slope decrease run-up and overtopping. This will be discussed in section 5.5.
As boundary condition for the calculation of wave run-up and overtopping one should use the hydraulic conditions at the toe of the structure (thus not on deep water). It has been shown in experiments that the spectral wave height and period \(H_{m0}\) and \(T_{m-1,0}\) provide the most accurate prediction of run-up and overtopping, also in non-standard cases such as double-peaked spectra and (very) shallow foreshores. If only information about the deep water conditions is available, the conditions at the toe of the structure can be calculated using a spectral nearshore wave transformation program, like SWAN or similar.
